Umění optimálního skladování
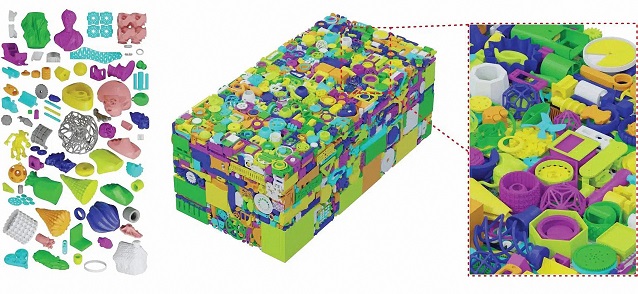Nový algoritmus vyvinutý vědci z MIT CSAIL může usnadnit umísťování různých objektů uvnitř vymezeného prostoru, s nadsázkou třeba při balení kufrů na dovolenou.
Problém optimálního způsobu hustého umístění 3D objektů různých tvarů a velikostí je klasifikován stupněm obtížnosti NP, což znamená, že jej prakticky není možné přesně vyřešit bez dlouhých výpočtových časů v závislosti na počtu kusů, které je třeba do určeného prostoru (např. kontejneru) vměstnat.
K významnému pokroku došlo nyní díky nové výpočetní metodě, která činí tento úkol lépe zvládnutelný. Tým vědců z MIT CSAIL a Inkbit (MIT spinout) představil techniku Scalable Spectral Packing (SSP), o které informoval v ACM Transactions on Graphics. Tato technika umožňuje vypracovat pořadí pevných 3D objektů a jejich umístění, kdy je jedním z možných přístupů např. začít s největšími objekty a končit nejmenšími. Pro usnadnění tohoto procesu je kontejner „voxelizován“, tzn., zobrazen 3D mřížkou složenou z malých krychlí (voxelů), z nichž každá může mít velikost jen kubický milimetr. Ty ukazují, které části kontejneru (resp. voxely) jsou již obsazeny a které jsou k dispozici. Rovněž předmět, který má být umístěn, je „voxelizován“ soustavou kostek stejné velikosti.
Kolizní metrika
Aby algoritmus zjistil dostupný prostor pro každý objekt, vypočte pro každý voxel hodnotu označovanou jako kolizní metrika, čímž zjistí počet obsazených voxelů, s nimiž se objekt překrývá. Objekt lze umístit jen na pozice, kde je překrytí nulové a nedochází k nežádoucím kolizím.
Dalším krokem je projít možná umístění a určit nejlepší dostupnou pozici pro daný objekt. Pro tento úkol slouží další voxelová metrika, aby lokálně maximalizovala hustotu objektů – měří mezery mezi objektem a stěnou kontejneru, nebo mezi objektem, který se přesouvá, a objekty v kontejneru již umístěnými, s cílem minimalizovat mezery mezi nimi. Systém připomíná hru Tetris, kde je úkolem nechat co nejméně prázdného místa.
To ale není vše
Co bylo zmíněno dosud, se týká předmětu, který je přemístěn při zachování pevné orientace v prostoru. Počítač ale může celý tento proces provést s mnoha různými orientacemi pro stejný objekt, dokud pro něj nenajde pozici, která nejlépe odpovídá danému prostoru.
Posledním úkolem je zajistit, že pro teoreticky ideální uspořádání může být každý předmět nejen skutečně usazen na přidělené místo, ale i to, že může být oddělen od ostatních objektů (např. při vybalování). To znamená, že pozice musí být „bez blokování“, proto je podmínkou vyloučení nežádoucích konfigurací.
To vše ale vyžaduje spoustu výpočtů, proto vědci mazaně použili nekonvenční řešení: rychlou Fourierovu transformaci (FFT). Jde o speciální matematickou techniku, která na problém balení nikdy předtím nebyla aplikována. Na rozdíl od nepraktického testování všech možných umístění objektů lze pomocí FFT problémy s kolizním překrytím voxelů a minimalizací mezer vyřešit ideální umístění pomocí relativně omezené sady výpočtů, což zrychluje balení o několik řádů.
V jedné z ukázek nový algoritmus efektivně umístil 670 objektů za pouhých 40 sekund, a dosáhl hustoty balení asi 36 %. Uspořádání zhruba desetkrát většího množství (6596) předmětů s hustotou balení 37,30 % trvalo dvě hodiny. Hustoty, které získává, dosahují téměř 40 % a jsou výrazně lepší a také rychlejší než ty, získané tradičními algoritmy.
Tento přístup maximalizující hustotu uložení má potenciál najít uplatnění v mnoha oblastech, např. pro skladové a expediční firmy, kde se různé předměty balí do krabic různých velikostí. Vědce však zajímají zejména aplikace v 3D tisku. Díly v aditivní výrobě se běžně vyrábějí v dávkách a umisťují na podložky, ovšem současné přístupy mají omezené využití objemu úložného prostoru – obvykle kolem 20 %. Pokud by se dokázala zvýšit hustota balení, bylo by možné zvýšit efektivitu tiskového procesu a tím snížit celkové náklady na vyrobené díly.
Steve Nadis
Foto: MIT CSAIL
41
